• Chapter 3 Annuities
  • 3.1 introduction:
  • 3.2 Annuities - immediate,
  • 3.3 Annuities - due
  • 3.4 Perpetuity
  • 3.5 Deferred annuities and values on any date
  • 3.6 Outstanding loan balance
    • Retrospective method:
    • Prospective method:
  • 3.7 Non-level Annuities
  • 3.8 Annuities with payments in geometry progression * :
  • 3.9 Annuities with payments in arithmetic progression + :
    • annuity-immediate:
    • annuity-due:
  • 3.10 Yield rate
  • 3.11 annuity symbols for non-integral terms
    • Drop payment
    • Balloon payment

Chapter 3 Annuities

3.1 introduction:

• Annuity is the series of payments made at specified intervals for a fixed or continent period.
  e.g. repayment of loan, or deposits to a retirement fund;
• Payment period , the interval.

3.2 Annuities - immediate,

Pay at the END of each payment period, receive first payment at the end of first payment period.

• Basic annuity immediate lasting $n$ period, with level payment $1.

• The Present value of basic annuity immediate equals the sum of the present value of the $n$ end-of-period payments:
  $v(1) + v(2) + \ldots + v(n)$.
  
  

  • when it is compound interest at an effective rate of $i$ per period, $v(t) = (1+i)^{-t}= v^t$
    therefore the sum is $v+v^2+v^3+\ldots+v^n$ .
    
    

• Geomatric series: $c+cr+c^2+ \ldots +cr^{n-1} = \frac{c(1-r^n)}{1-r}$.
  
  → the present value of the basic annuuity-immediate lasting $n$ interest periods
  
  $v+v^2+v^3+\ldots+v^n=\frac{v(1-v^n)}{1-v}=\frac{1-v^n}{i}$.
  
  

• Present value symbol a_{${\overline{n|}}i$}.
  
  

• Compound interest annual effective rate:
  a _{${\overline{n|}}i$}$=v+v^2+v^3+\ldots+v^n=\frac{1-v^n}{i}$.
  
  

• Final payment is S_{${\overline{n|}}i$}, measure teh value $n$ period after.
  

• When $a(n)=(1+i)^n$, compound interest rate, S_{${\overline{n|}}i$}$=(1+i)^n$, $a$ _{${\overline{n|}}i$}, and $a$ _{${\overline{n|}}i$} $=v^n$S_{${\overline{n|}}i$}.
  
  

• In General: S_{${\overline{n|}}i$}$=a(n)$ $a$ _{${\overline{n|}}$}, and $a$ _{${\overline{n|}}$} $=v(n)$ S_{${\overline{n|}}$}.
  
  

• S_{${\overline{n|}}i$}$=\frac{(1+i)^n-1}{i}$
  
  

• PMT ＝ FV／a_{${\overline{n|}}i$}
  If future value (Loan)is to be repaid by n level end-of-period PMT, with effective interest rate for the payment period is $i$.

• PMT ＝ FV／S_{${\overline{n|}}i$}
  If future value is to be accumulated by n level end-of-period PMT, with effective interest rate for the payment period is $i$.

• 

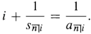
• Calculator, calculate without BGN on the top, meadning the payment is given at the end of period. See page p120.

  • I/Y, interest rate per year, nominal interest rate, as percentage;
  • P/Y, payments per year;
  • C/Y, the number of interest conversion period per year.

3.3 Annuities - due

Pay at the BEGINNING of each payment period.

• ${\ddot {a}}$ _{${\overline{n|}}i$}, represents the value at (first payment time) that lasts $n$ periods. (present value).

• ${\ddot {S}}$ _{${\overline{n|}}i$}, represents the value (at the end) that lasts $n$ periods.

• ${\ddot {S}}$ _{${\overline{n|}}i$} $=(1+i)^n$ ${\ddot {a}}$ _{${\overline{n|}}i$}, and ${\ddot {a}}$ _{${\overline{n|}}i$} $=v^n$ ${\ddot {S}}$ _{${\overline{n|}}i$}.
  
  

• In General: ${\ddot {S}}$ _{${\overline{n|}}$}$=a(n)$ ${\ddot {a}}$ _{${\overline{n|}}$}, and ${\ddot {a}}$_{${\overline{n|}}$} $=v(n)$ ${\ddot {S}}$ _{${\overline{n|}}$}.
  
  

• Compound interest annual effective rate:
  ${\ddot {a}}$ _{${\overline{n|}}i$}$=v+v^2+v^3+\ldots+v^n=\frac{1-v^n}{d}$.
  
  

• $v+v^2+v^3+\ldots+v^{n-1}=\frac{1(1-v^n)}{1-v}=\frac{1-v^n}{d}$.

• ${\ddot {S}}$ _{${\overline{n|}}i$}$=\frac{(1+i)^n-1}{d}$
  
  
  Note:
  
  

• ${\ddot {a}}$ _{${\overline{n|}}i$} $=(1+i)$ a_{${\overline{n|}}i$}
  
  ${\ddot {S}}$ _{${\overline{n|}}i$} $=(1+i)$ S_{${\overline{n|}}i$}
  
  

• ${\ddot {a}}$ _{${\overline{n|}}i$} $=$ a_{${\overline{n-1|}}i$} $+1$
  
  
  ${\ddot {S}}$ _{${\overline{n|}}i$} $=$ S_{${\overline{n+1|}}i$} $-1$

3.4 Perpetuity

annuity with an infinity term.

• infinite payment periods, ${\ddot {a}}$ _{${\overline{∞|}}i$} $=$ a_{${\overline{∞|}}i$} $+1$

• ${\ddot {a}}$ _{${\overline{∞|}}i$} $=\frac{1}{d}$

• a_{${\overline{∞|}}i$} $=\frac{1}{i}$
  
  

3.5 Deferred annuities and values on any date

• A wait of more than one payment period for a payment. retrospective method
• times $v^n$

3.6 Outstanding loan balance

how to find loan balance at an intermediate date between the loan origination date and the date of the final payment.

Retrospective method 回顾法:

$L$, the amount to be paid at the end of $n$ times period.
$i$, effective interest rate per payment,
loan balance at time $k$ is $L(1+i)^k$.
$OLB_k$ the loan balance at the end of k payment period(right after k payment),
$Q$ is each payment of first $k$ period.
→ $OLB_k=L(1+i)^k-Q$ S_{${\overline{n|}}i$}.

Prospective method:

$OLB_k$, the remaining value after time $k$ payment.
$Q$, the amount of all but last payment
$R$, last payment.
$OLB_k=Q$ a_{${\overline{n-k-1|}}i$} $+R(1+i)^{n-k}$.
when all payments are equal $OLB_k=Q$ a_{${\overline{n-k|}}i$}.

3.7 Non-level Annuities

use CASHFLOW.

3.8 Annuities with payments in geometry progression * :

• $(1+g)$ times its predecessor, $i$, effective interest rate for the payment period. $n$, payment period.
  annuity one period before the first payment is
  
  $P(\frac{1- \frac{1+g}{1+i}^n }{i-g})$
  
  

3.9 Annuities with payments in arithmetic progression + :

At the end of $j^{th}$ interest period, $P$, the first payment, increased by constant amount of $Q$,

annuity-immediate:

PV = $(I_{P,Q} a)$_{${\overline{n|}}i$} $=P a$ _{${\overline{n|}}i$} + $\frac{Q}{i}($ a _{${\overline{n|}}i$} $-nv^n)$.

FV = $(I_{P,Q} S)$_{${\overline{n|}}i$} $=P S$ _{${\overline{n|}}i$} + $\frac{Q}{i}($ S _{${\overline{n|}}i$} $-n)$.

• when $P=Q=1$, PV = $(Ia)$_{${\overline{n|}}i$}, FV = $(I S)$_{${\overline{n|}}i$}.
• when $P=n, Q=-1$, decreasing annuity, payment is $n, n-1, n-2, \ldots 2,1$
  
  $(D a)$_{${\overline{n|}}i$} $=n$ a_{${\overline{n|}}i$} $-\frac{1}{i}($ a_{${\overline{n|}}i$} $-nv^n)$ =$(n-a$ _{${\overline{n|}}i$} $)/i$
  
  $(D S)$ _{${\overline{n|}}i$}$=(D a)$ _{${\overline{n|}}i$} $(1+i)^n$.
  
  

annuity-due:

PV = $(I_{P,Q} {\ddot {a}})$_{${\overline{n|}}i$} $=P {\ddot {a}})$ _{${\overline{n|}}i$} + $\frac{Q}{d}(a$ _{${\overline{n|}}i$} $-nv^n)$.

FV = $(I_{P,Q} {\ddot {S}})$_{${\overline{n|}}i$} $=P {\ddot {S}})$ _{${\overline{n|}}i$} + $\frac{Q}{d}(s$ _{${\overline{n|}}i$} $-n)$.

• when $P=Q=1$,
  PV = $(I {\ddot {a}})$_{${\overline{n|}}i$},
  
  FV = $(I {\ddot {S}})$_{${\overline{n|}}i$} $=({\ddot {S}}$ _{${\overline{n|}}i$}$-n)/d$;

• when $P=n, Q=-1$, decreasing annuity, payment is $n, n-1, n-2, \ldots 2,1$
  PV = $(D {\ddot {a}})$_{${\overline{n|}}i$} $=(n-a$ _{${\overline{n|}}i$} $)/i$,

Note:
$(Ia)$_{${\overline{n|}}i$} $+(D a)$_{${\overline{n|}}i$} $=(n+1)a$_{${\overline{n|}}i$},
$(I {\ddot {a}})$_{${\overline{n|}}i$} $+(D {\ddot {a}})$_{${\overline{n|}}i$} $=(n+1){\ddot {a}}$_{${\overline{n|}}i$}

3.10 Yield rate

• guess and check
• Newton’s method
• TVM worksheet, use CASHFLOW.

3.11 annuity symbols for non-integral terms

1. positive real number $r$, then, we have $a$_{${\overline{r|}}i$} $=\frac{1-v^{r}}{i}$,
   let $L$ be the total amount and $Q$ be end-of-period payment, with $i$ effective interest rate.

2. then when we calculate $r*lnv =ln(1-\frac{iL}{Q})$, $r$ may be not an integer.

3. Therefore we re-write $r=n+f$, where n is an integer and $0≤f≤1$.

4. $L=Qa$_{${\overline{n|}}i$} $+Q(\frac{(1+i)^f-1}{i})v^r$

Drop payment

• make $n$ payment of $Q$, then make the $n+1$ -th payment of $Q(\frac{(1+i)^f-1}{i})(1+i)^{1-f}$
  The last time smaller payment is drop payment.
  

Balloon payment

• make $n-1$ payment of $Q+Q(\frac{(1+i)^f-1}{i})v^f$.
  The last larger payment is ballon payment.