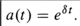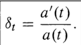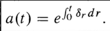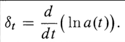
| Investment opportunities theory | Time preference theory |
|---|---|
| that you borrow money from bank, the borrowed money allows you to make more money, so you pay a bit back to the bank, as interest. | that the option to use money immediately, to lend the money out. interest compensates a lender for the loss of choice (immediate money), and the risk of landed money is lost. |
Unit of money : dollar, euros, yen, gold pieces.
Principal the investment amount $K of money, or the amount of money borrowed.
Unit of time : year, month, day, quarter. Time t = 0, is the initial financial transaction, meaning $K is invested at t = 0.
| Amount function | principle | |
|---|---|---|
| Accumulation function | a(t) | principle is $1. |
NOTE:
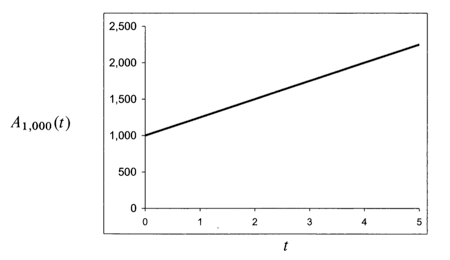
An investment of grows by a constant amount of each year for five year.
.
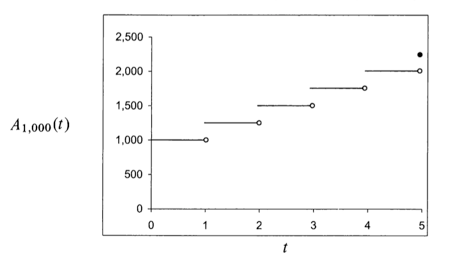
| interest paid continuously | interest paid at the end of every year |
|---|---|
 |
 |
Effective Interest Rate for the internal :
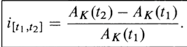 |
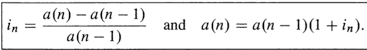 |
|---|
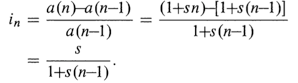
A borrows $5000 from B on October 14, 1998 at 8% exact simple interest and repay the loan on May 7, 1999. What is the amount of A’s repayment?
| Exact simple interest | Ordinary simple interest |
|---|---|
| Duration of the loan in days : add exact days to 205 | duration of the loan in days: 6*30 + (30-14) + 7 = 203 |
| repayment = | repayment = |
Compound interest accumulation function at interest rate .
Greatest integer function, , greatest integer , is a floor function.
deposit $12000 at bank, Money receive after 6.5 years is,
| compound interest accumulation function | accumulation function |
|---|---|
Discount rate, investor lends $K for one period at a discount rate D, then the borrower will have to pay $K * D in order to receive the used of $K. The quantity $KD is called the amount of discount.
Effective discount rate,
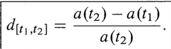 |
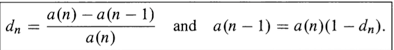 |
|---|
growth of money is governed by the accumulation function a(t) = (1.05)^(t/2) (1+ 0,025t). find d4 and i4 .
.
discount function,
discount factor , compound interest accumulation function , then we define discount factor .
present value, present value of $L to be received in year t
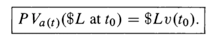
Net Present Value, sequence of investment returns received at time 0, .
use calculator, enter CASH FLOW value then press NPV
| amount function | $K invested by simple discount at rate d | |
|---|---|---|
| simple discount accumulation function | $1 is invested at rate d |
effective discount rate,
, .
For borrower, choose low annual effective interest rate, low annual effective discount rate.
bank credit interest more than once per year, m times per year.
nominal (annual) interest rate of , convertible, compounded, or payable M times per year.
i is APY, annual percentage yield.
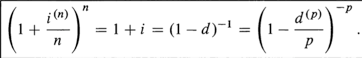
2nd-ICONV to calculate NOM and EFF
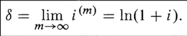 and
and
 , and
, and