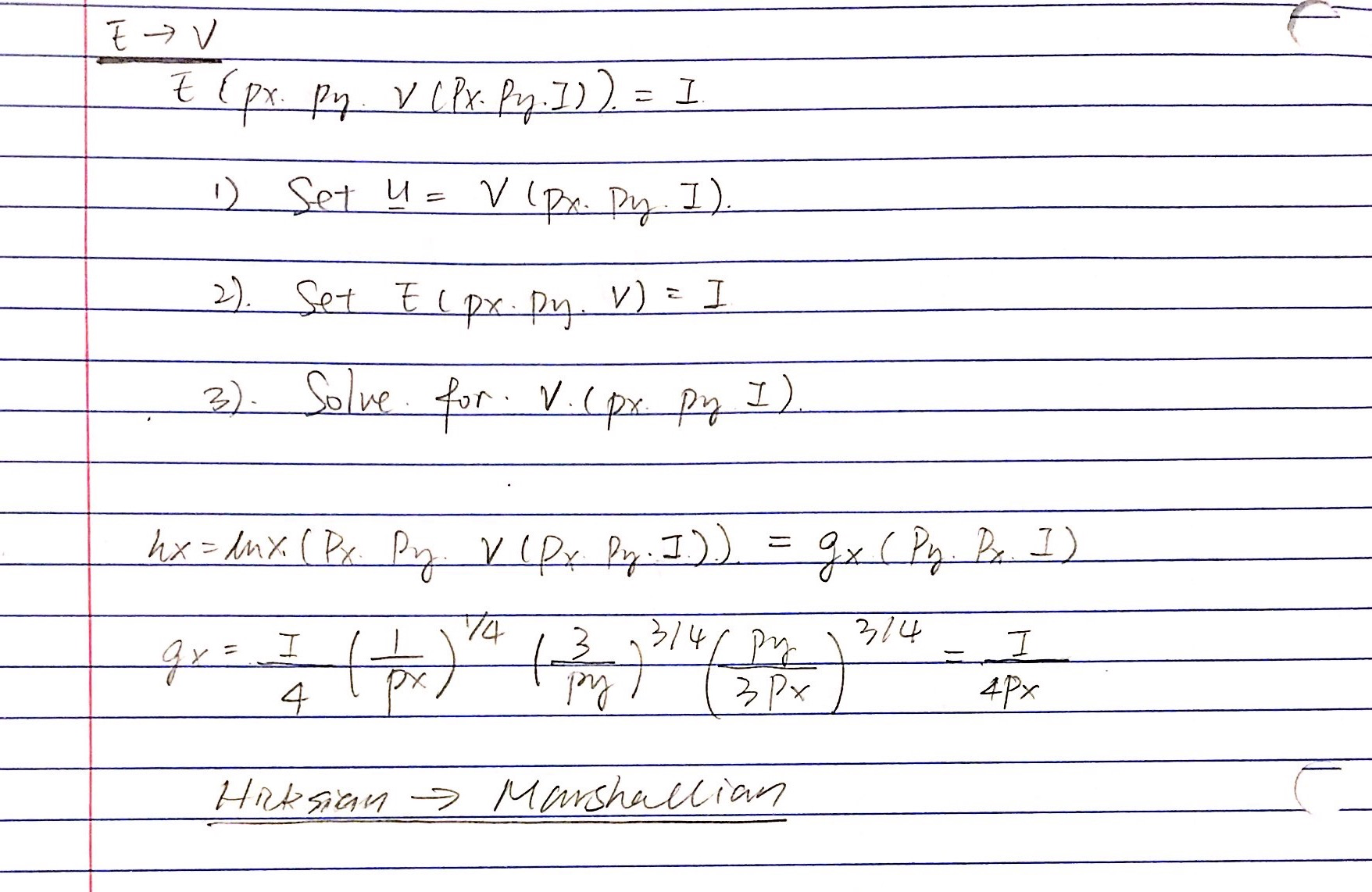• Chapter 3 Preference and Utility
  • Rational Choices
  • Utility:
  • Trade and Substitution:
    • indifference curves
    • Transitivity
    • Convexity
    • Example of utility functions
    • Homothetic Preference:
  • The many good case:
• Chapter 4, Utility Maximization and Choices
  • The Budget Constraint:
  • First Order condition for a maximum.
  • Second Order condition for a maximum
    • Corner Solutions
    • Marshallian Demand Funciton
    • Perfect Substitution Example:
    • Perfect Complements Example:
  • Indirect Utility Function:
  • Expenditure Minimization
    • Properties of expenditure functions $y=-\frac{p_x}{p_y}x+\frac{E}{p_y}$
    • Hicksian Demand Function
  • Summary
    • Marshallian-Demand-Funciton → Hicksian-Demand-Function

Chapter 3 Preference and Utility

how people make decisions.

Rational Choices

• Completeness:
  • ‘‘A is preferred to B,’’
  • ‘‘B is preferred to A,’’
  • ‘‘A and B are equally attractive.’’
• Transitivity:
  • ‘‘A is preferred to B, B is preferred to C, so A is preferred to C’’
• Continuity:
  • If ‘‘A is preferred to B’’, then situations suitably ‘‘close to’’ A must also be preferred to B
    
    

Utility:

• Axioms satisfied → utility function.
• Utility ranks the desirability of consumption, not the happiness , nor depend on people;

Example:

→ U(B) > U(A)$ for most people. (the desire of B)

→ Imply a increasing function.

Trade and Substitution:

• Indifference Curve shows a set of consumption bundles among which the individual is indifferent.

• Marginal rate of substitution, MRS, the negative of the slope of the indifference curve at any point. $MRS=-\frac{dy}{dx}$.

  • measures individuals willingness to trade $y$ for $x$;
  • MRS changes as $x$ and $y$ change.

Example: All $x$, $y$ such that $U(x, y) = K$;

Total differential $U' = 0$;

$d U = \frac {\partial L}{\partial x} + \frac {\partial L}{\partial y} = 0$

indifference curves

Transitivity

no intersection.

Convexity

• instead of consuming the extreme value, taking average of the two, → well balanced bundles are preferred.
  $αA+(1-α)b >A, 0<α<1$ line AB is higher utility than the indifference curve.

Example of utility functions

• Cobb Douglas:
  • $U(x,y) = x^α v^β, α,β>0$, $U(x,y)=α*logx + β*logy$,
  • MRS = $\frac{U_x}{U_y}$, where $U_x = \frac{α}{x}$,$U_y = \frac{β}{y}$
  • Therefore MRS $=\frac{α}{β}* \frac{y}{x}$

$U(F,C,B)=6ln F + 2ln C + lnB$, and given: $P_F = 5, P_C = 20,P_B = 50, I =500$,
→ $5F+20C+50B=500$
therefore, $L=6ln F + 2ln C + lnB + λ（500－5F－20C－50B)$
$\frac{∂L}{∂F} = \frac{6}{F}=5λ$
$\frac{∂L}{∂B} = \frac{1}{B}=50λ$
$\frac{∂L}{∂C} = \frac{2}{C}=20λ$
therefore:
$MRS_{B,F} = \frac{6}{F} * B = 5/50 = \frac{P_F}{P_B}$
$MRS_{C,F} = \frac{6}{F} * \frac{C}{2} = 5/20 =\frac{P_F}{P_C}$
$MRS_{C,B} = \frac{1}{B} * \frac{C}{2} = 50/20 =\frac{P_B}{P_C}$
Tangent condition $MRS = \frac{U_x}{U_y} = \frac{P_x}{P_y}$
(holds to many goods)

• Perfect substitutes:

  • $U(x,y)=Ax+By$
    infinity numbers of solution, fails convexity.
  • MRS is a constant: $MRS =\frac{A}{B}$, since $U_x = A, U_y = B$.
    no larganian can be applied
  • coins, bill, that substitutes with same rate.
    
    

• Perfect Complements:

• $U(x,y)=min(Ax,By)$.

• The Angle gives the right combination, any other point does not change the utility.

  • infinite - vertical slope: no use for extra goods;
  • zero - horizontal slope: no need to give up the other goods for extra goods;
  • slope at the angle point, may varies.
    * Keep x constant, and increasing y does not increase utility. Increase both x, y will increase the utility.
    
    

• Constant Elasticity of substitution:
  previous three are special cases of CES.
  $δ=1, 0, -∞$ .

Homothetic Preference:

• MRS depends only on the ratio of the amount consumed of two goods.
  all indifference curves have the same shape
  • perfect substitution: MRS is same everywhere;
  • perfect complements MRS $=∞$

$U(x,y)=x + ln y$
Homothetic Preferences: MRS $=\frac{α}{β}\frac{y}{x}=e^{\frac{x}{y}}$
Non Homothetic Preferences: MRS = y

The many good case:

$U(x_1,x_2,\ldots, x_n)$ = K, Constant

Chapter 4, Utility Maximization and Choices

1. Determine all available choices by given income, to form budget constrain.
2. then choose the one we prefer, indifference curves.

The Budget Constraint:

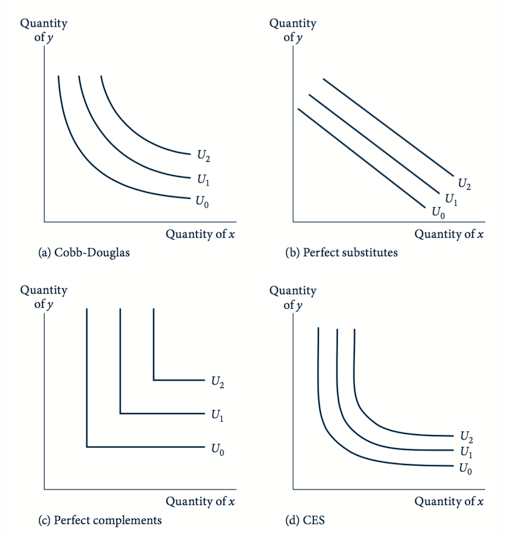
Set $x,y$ two goods, $p_x, p_y$ are the price of two goods, income $I$, then we have $p_x x+ p_y y≤I$

1. when $x=0, p_y y = I,y= \frac{I}{p_y}$, vertical intersection.

2. when $y=0, p_x x = I,x= \frac{I}{p_x}$, horizontal intersection.

3. Connect the points then we get the bundles we can choose.
   $y= -\frac{p_x}{p_y} + \frac{I}{p_y}$, slope is negative.

Example:
$x$ = drink, $y$ duck, $p_x = $100, p_y$ = 20/lB

then we have $-\frac{p_x}{p_y}$ = 100/20 = -5, meaning that for one more drink we receive, we need to give up one pound of duck.

First Order condition for a maximum.

• C: Outside the budget constrain, happier but cannot afford;
• B: Tangent point of utility curve (consumption bundle) and indifference curve.
• A: Inside the budget constrain, can afford but not max happiness.

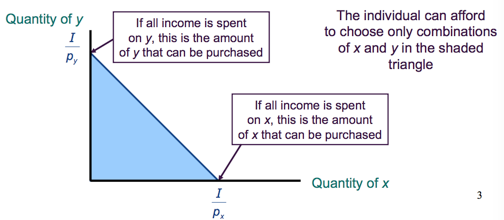
• Utility is maximized at B.
  The budget constrain and the tangent line have same slope.

  • slope of budget constraint $=-\frac{p_x}{p_y}$

  • slope of indifference curve $\frac{dy}{dx}= -\frac{ \partial U}{ \partial X} / \frac{ \partial U}{ \partial y}=-MRS$

  • then we have $= \frac{p_x}{p_y} = \frac{ \partial U}{ \partial X} / \frac{ \partial U}{ \partial y}=MRS$
    

Example:
Need to find the Max of $U(x, y)$, $p_y y+p_x x=I$

Then we can set up $L=U(x, y)+ \lambda(I-p_y y-p_x x)$

Take Partial derivatives equals Zero, so that

$\frac{ \partial L}{ \partial x}-\frac{ \partial U}{ \partial x} = \lambda p_x =\frac{ \partial L}{ \partial y}-\frac{ \partial U}{ \partial y} = \lambda p_y = \frac{ \partial L}{ \partial \lambda } = I-p_y y-p_x x = 0$

→ $\frac {p_x}{p_y}=MRS$;

Second Order condition for a maximum

• MRS is diminishing: Convax → Always have a maximum;

• MRS is not diminishing: Check second order derivatives;

• When increase x, MRS is flatter, how to check:
  $\frac{ \partial MRS}{ \partial x}= \partial {\frac{MU_x}{MU_y}}/ \partial x <0$
  
  

Corner Solutions

Maximize utility by choosing to consume only one of the goods, where the indifference curve is not tangent to the budget constraint.

• negative consumption - sell (not common);

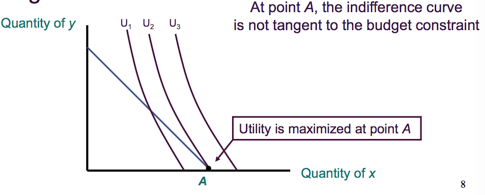
in this class, when we get the max from first order derivative, then there is no need to check second order, except 2 following situations:

Marshallian Demand Funciton

Let $x_1$ = Food with $p_1, x_2$ = other goods with $p_2$, the utility function is $U(x_1,x_2)= x_1^{0.5} + x_2^{0.5}$

→ then we can set up: $L= x_1^{0.5} + x_2^{0.5} = \lambda (I- p_1-p_2)$

→ set first order derivative equals zero:

$\frac{ \partial L}{ \partial x_1} = 0.5 x_1^{-0.5} - \lambda p_1 = 0$

$\frac{ \partial L}{ \partial x_2} = 0.5 x_2^{-0.5} - \lambda p_2 = 0$

$\frac{ \partial L}{ \partial \lambda } = I-p_1 x_1 - p_2 x_2$

→ $\frac{x_2}{x_1} ^{0.5} = \frac{p_1}{p_2}$， plug in and solve for $x_1$ and $x_2$

→ $x_1^* = \frac{I}{p_1(1+\frac{p_1}{p_2})} = g_1(p_1, p_2, I)$, similar: $x_2^* = \frac{I}{p_2(1+\frac{p_2}{p_1})} = g_2(p_1, p_2, I)$

$g_1, g_2$ are Marshallian Demand Funciton

Then we check second order derivatives: $\partial x_2^* / \partial p_2 = \partial g_2(p_1, p_2, I) / \partial p_2<0$

Perfect Substitution Example:

• indifference curve is flatter than the budget constraint:
  $x_1^* = \frac{I}{p_1}, x_2^* = 0$;

• indifference curve is steeper than the budget constraint:
  $x_2^* = \frac{I}{p_2}, x_1^* = 0$;

Given $U(x_1, x_2) = 0.4x_1 + 0.8x_2$
(How to find out the indifference curve is flatter or steeper?)

slope indifference curve: $- \frac{dx_1}{dx_2}=- \frac{ \partial U}{ \partial x_2} / \frac{ \partial U}{ \partial x_1}= -2$

$\frac{p_2}{p_1}<2, x_2^* = \frac{I}{p_2}, x_1^* = 0$

$\frac{p_2}{p_1}>2, x_1^* = \frac{I}{p_1}, x_2^* = 0$

$\frac{p_2}{p_1}=2$

Perfect Complements Example:

Given $U=min(x_1,2x_2)$, we need to find the max of U, min $(x_1, 2x_2), and we know p_1 x_1 + p_2 x_2 = I$
→ set $x_1 = 2x_2$, and on the budget constraint.
→ solve:
$x_1 = 2x_2$ and $p_1 x_1 + p_2 x_2 = I$.

Indirect Utility Function:

• How the welfare/utility change when the price and income vary. Need to find the optimal consumption, replace in Utility and we get indire utility function $= U(x_1^* (p_1,...,p_n, I), x_2^* (p_1,...,p_n, I))$, denoted as $V(p_1,...,p_n, I)$.

• Enable us to determine the effect of government policies on the welfare/happiness of an individual.

Example:
$c,l,p,w$, and given $U(c,l) = \alpha lnc + \beta ln$
so we can calculate $c^* = \frac{ \alpha}{ \alpha + \beta } \frac{i}{p}, l^* =\frac{ \beta}{ \alpha + \beta} \frac{i}{w}$

$V(p,w,I)=U(c^* , l^* ) = \alpha ln(\frac{ \alpha}{ \alpha + \beta } \frac{i}{p})+\beta ln(\frac{ \beta}{ \alpha + \beta} \frac{i}{w})$

→ $V=\alpha ln \frac{ \alpha}{ \alpha + \beta }+ \beta ln \frac{ \beta}{ \alpha + \beta }+(\alpha+\beta)lnI-\alpha lnp - \beta lnw.$

Example:
Policy: Progresa pays 200$ a year to eligible families that pay money for education.(Mexico reduces poverty).
Known: Average income: 13200 pesos = 1320$ (1 peso = 0.1$), Hourly wage = 0.1$, Price of consumption: 0.1$, Cobb Douglas Utility Function, $\alpha = 0.5, \beta = 0.5$

Before government involves:
$V(0.1, 0.1, 1320)= 0.5 ln 0.5 + 0.5 ln0.5 + ln 1320 - 0.5 ln 0.1 - 0.5 ln 0.1 = 8.8$

With the 200$ cash from government:
$V(0.1, 0.1, 1320+200)= 0.5 ln 0.5 + 0.5 ln0.5 + ln (1320+200) - 0.5 ln 0.1 - 0.5 ln 0.1 = 8.94$

Price subsidy → 200 per family
$c^* = \frac{ \alpha}{ \alpha + \beta } \frac{i}{p} = \frac{0.5}{1}\frac{1320}{0.1} = 6600$, $\tau = subsidy$ → the price of goods now is changed to $p-\tau$.

$c^* = \frac{ \alpha}{ \alpha + \beta } \frac{i}{p} = \frac{0.5}{1}\frac{1320}{0.1- \tau} = 6600$ $\tau c^* = 200$

∴ $\tau = 0.02326, c^* = \frac{660}{0.1-0.02326}=8600$, → $\tau c^* =$200$
→ $V(0.1-0.02326, 0.1, 1320)= 0.5 ln 0.5 + 0.5 ln0.5 + ln 1320 - 0.5 ln (0.1-0.02326) - 0.5 ln 0.1 = 8.92$


Compare the above results:

• Price subsidy
  • increase the purchasing power of the consumer;
  • biases people’s choices toward consumption.
    
    
• Income transfer does not have the second negative effect.
  
  

Expenditure Minimization

• Minimize the expenditure subject to a minimum level of utility that the consumer must obtain.

Example:
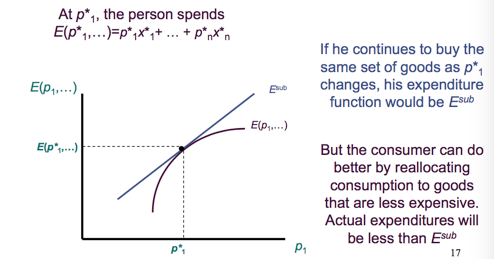
let $x, y$ be two goods and $p_x, p_y$ be their price, the Expenditure $=p_x x+p_y y$ , with slope $=\frac{p_x}{p_y}$, and therefore $y=\frac{p_x}{p_y}x + \frac{E}{p_y}$
then the problem becomes to solove the minimum for: min $=p_x x+p_y y$, $U(x,y)≥ U_-$

$L=p_x x+p_y y + \lambda(U_- -U(x,y))$

$\frac{\partial L}{\partial x}=p_x- \lambda \frac{\partial U}{\partial x}=0$

$\frac{\partial L}{\partial y}=p_y- \lambda \frac{\partial U}{\partial y}=0$

$\frac{\partial L}{\partial \lambda}=U-U(x,y)=0$

→ $\frac{p_x}{p_y}=MRS$

Properties of expenditure functions $y=-\frac{p_x}{p_y}x+\frac{E}{p_y}$

• Homogeneity(of degree one):
  All prices double, utility remains same, then the expenditure will double.
• Nondecreasing in price:
  • $\frac{\partial E}{ \partial p_i}≥0$ for every good
• Concave

  • Continue to buy same set of goods as $p_1^{* }$ changes, his expenditure function would be $E^{sub}$.

  • Actual expenditure is less expensive than $E^{sub}$ by reallocating consumption to goods.

    

Hicksian Demand Function

$E(p_x^* , p_y^* , U) = p_x x^* +p_y y^{* }$

$U(c,l)=c^{0.5}l^{0.5}$
min pc+wl → $c^{0.5}l^{0.5}≥ U_-$
→ $p=\lambda \frac{\partial L}{\partial c}$ $w=\lambda \frac{\partial L}{\partial l}$

$U(c,l)=c^{0.5}l^{0.5}

$c=\frac{w}{p}l$
$U = (\frac{w}{p}l)^{0.5}L^{0.5}$
→
$l^* = U \frac{p}{w}^{0.5}=h_l(p,w,U)$
$c^* = U \frac{w}{p}^{0.5}=h_c(p,w,U)$
$E(p_x^* , p_y^* , U) = p_x x^* +p_y y^*$

$E(p_x^* , p_y^* , U)=p* h_c(p,w,U) + w*h_l(p,w,U) = 2(pw)^{0.5}U$

Summary

1. Utility Maximization

   • Maximize the utility subject to a budget constraint. → get Marshallian Demand funciotn.
   • Substitute the Marshallian-Demand-Funciton in the utility function to get an indirect utility function.
   • Indirect utility function measure the highest level of utility we can chieve with given price and income.
     
     

2. Expenditure Minimization

   • Minimize expenditure subject to a utility constraint. → Hicksian demand function.
   • Substitute the hicksian-demand-function in expenditure, to measure the lowest expenditure required to achieve with a given utility.
     
     

Example:
$U=min(\alpha x, \beta y)$
$min(\alpha x, \beta y)=U_-$
$min(\alpha x, \beta y)=\alpha x = \beta y$
→ $\alpha x = U_-$

Example: from last lecture.
$E(p,w,U_-)=I, V(p,w,I)=U_-$

1. • start from $E(p,w,U_-)=I$, derive $V(p,w,I)=U_-$.
   • Utility Function is cobb dogg, $E(p,w,U_-)=2(pw)^{0.5}U_-$
     $I = 2(pw)^0.5U_-$
   • Solve for $U_-$: $U_- = \frac{I}{2(pw)^{0.5}}$, → $V(p,w,I)=U_-=\frac{I}{2(pw)^{0.5}}$
2. • start form $V(p,w,I)=U_-$, derive $E(p,w,I)=U_-$
     $V(p,w,I)= \frac{I}{2(pw)^{0.5}}$, → $E(p,w,I)=2(pw^{0.5}U_-)$

Marshallian-Demand-Funciton → Hicksian-Demand-Function

$c^* = \frac{1}{2} \frac{I}{P}, l^* = \frac{1}{2} \frac{I}{w}$
→ derive $V(p,w,I)$ → derive $E(p,w,U_-)$

Then we get $E(p,w,U_-)=2(pw)^{0.5}U_-$, therefore $I=2(pw)^{0.5}U_-$

$c^* = \frac{1}{2} \frac{2(pw^{0.5}U_-)}{P}=(\frac{w}{p})^{0.5}$

$l^* = \frac{1}{2} \frac{2(pw^{0.5}U_-)}{w}=(\frac{p}{w})^{0.5}$